How to approximate difficult-to-compute probability densities is an important problem in statistics. Variational Inference (VI) is a statistical inference framework that addresses this problem using optimization. This allows the use of it along with modern and fast optimization techniques which is ideal to approximate probability density functions of large datasets and complex models.
In this post I’m going to review Variational Inference, explaining the concepts that it involves, its derivation from the variational methods and its implications in the bayesian inference problem and in current machine learning techniques. I’m planning to write a full series on different bayesian machine learning methods, and Variational Inference is a core concept for them.
Bayesian modeling and inference
Let’s start by establishing the bayesian modeling, bayesian inference and the involved variables. Given some observable random variable \(\textbf{x}=x_1,..x_n\) and a hidden random variable \(\textbf{z}=z_1,..z_m\), bayesian models search to explain the observable data \(\textbf{x}\) by the hidden variable \(\textbf{z}\). This relation can be stated by Bayes’s Theorem.
$$ \begin{equation} p(\textbf{z|x}) = \frac{p(\textbf{z}, \textbf{x})}{p(\textbf{x})} = \frac{p(\textbf{x|z})p(\textbf{z})}{p(\textbf{x})} \end{equation} $$
The conditional probability density or posterior p(\textbf{z|x}) can be interpreted as the posterior belief of the prior \(p(\textbf{z})\), the update of it, after the data \(\textbf{x}\) is observed. In this setting, bayesian models draw from the prior or latent space \(p(\textbf{z})\), and relate it to the observable data through the likelihood \(p(\textbf{x|z})\), normalizing by the marginal likelihood or evidence \(p(\textbf{x})\).
Every parameter of the model is treated as a random variable and we impose information about these distributions through the prior. Bayesian inference for its side, searches to estimate the posterior \(p(\textbf{z|x})\). To perform Bayesian Inference, we need to compute the marginal likelihood \(p(\textbf{x})\) which formula is shown below.
$$ \begin{equation} p(\textbf{x}) = \int p(\textbf{z}, \textbf{x}) d\textbf{z} = \int p(\textbf{x}| \textbf{z})p(\textbf{z}) d\textbf{z} \end{equation} $$
The evidence \(p(\textbf{x})\) is an interesting measure because it can tell us how well the actual model can represent our data and can be directly used to compare different models. The problem with this formulation is that the posterior \(p(\textbf{z|x})\) is generally intractable, as also is the computation of the marginal likelihood by the integration of eq. \((2)\). Due to this, we are forced to search for approximation techniques to estimate both distributions. Sampling methods, particularly Markov Chain Monte Carlo (MCMC) algorithm, is one of the prefered ways to perform statistical inference. It converges asymptotically to the true posterior making it a good option when accurate solutions are needed. However, MCMC is computationally expensive making it not suitable in the case of large datasets or when the models are too complex.
A Small Point on Variational Methods
Variational methods are used for approximation in a different number of areas, such as quantum mechanics, finite element analysis and statistics. They turn a complex problem into a simpler one by decoupling the degrees of freedom of the complex problem at expenses of extending it adding extra parameters, we call them variational parameters.
Let’s clarify this definition with a small example from Jordan, Michael I., et al (1999). Take the natural logarithm function. It can be variationally redefined by the following equation.
$$ \begin{equation} \ln(x) = \underset{\lambda}{\min}\{\lambda x - \ln(\lambda) - 1\} \end{equation} $$
Without much effort we can check that the function under the brackets is minimized by \(\lambda^\ast=\frac{1}{x}\), and that by evaluating it at this optimal value, the equivalence is confirmed. Notice that for a fixed \(x\) we have turned the logarithm function into a linear function of the variational parameter \(\lambda\). More importantly, we can see that the variational function is an upper bound for the \(\ln(x)\), only touching the logarithm function at the optimal value of \(\lambda\) for the corresponding \(x\). This is much easier to see graphically in the figure below.
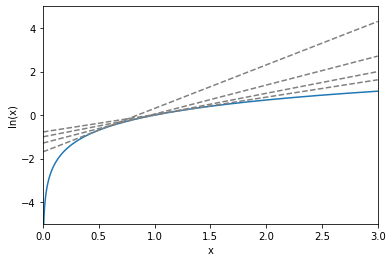
In the paper, it’s possible to follow the same development for other functions which are not necessarily convex ones, as the logistic function. Showing, that the variational model behaves as a lower or upper bound of the extended function. How this connect with the problem of bayesian inference and the intractables posterior \(p(\textbf{z|x})\) and marginal likelihood \(p(\textbf{x})\)? In the same way as we have done for the logarithm, we can extend our distributions using variational parameters. The variational methods will behave as lower/upper bounds to our model and Variational Inference will be a tool to find the optimal parameters.
Variational Inference
Instead of using sampling, Variational Inference transforms the inference problem into an optimization problem. By finding the optimal variational parameters, VI aims is to approximate the posterior \(p(\textbf{z|x})\), solving the bayesian inference problem, and as a by-product also estimates the marginal likelihood \(p(\textbf{x})\) which is the solution to the learning problem.
The idea behind VI is quite straightforward. First, we posit a family of distributions \(q(\textbf{z})\in\mathcal{Q}\) all with free variational parameters. This family is imposed over the latent space where each candidate \(q(\textbf{z})\in\mathcal{Q}\) is an approximation of the posterior. Then, we just search for the variational posterior or variational density \(q^{\ast}\) that minimize the Kullback-Leibler (\(\text{KL}\)) divergence against the true conditional posterior \(p(\textbf{z}|\textbf{x})\).
$$ \begin{equation} q^\ast(\textbf{z}) = \underset{q(\textbf{z}) \in \mathcal{Q}}{\text{argmin}}\ \text{KL}(q(\textbf{z})||p(\textbf{z}|\textbf{x})) \end{equation} $$
\(\text{KL}(q||p)\) is an information theory measure that compares two distributions. It can be interpreted as the loss of information due to the assumption that some data is distributed by \(q\) instead of the true distribution \(p\). I won’t go any deeper on it but if you want to know more, I recommend you this blog. To compute the \(\text{KL}\) divergence we face again the problem of computing first the marginal likelihood \(p(\textbf{x})\).
$$ \begin{align} \begin{split} \text{KL}(q(\textbf{z})||p(\textbf{z|x}))&\triangleq \sum q(\textbf{z})\log\frac{q(\textbf{z})}{p(\textbf{z|x})}\\ &= \mathbb{E}_q\Big[\log\frac{q(\textbf{z})}{p(\textbf{z|x})}\Big]\\ &= \mathbb{E}_q \Big[\log\frac{q(\textbf{z})p(\textbf{x})}{p(\textbf{z},\textbf{x})}\Big]\\ &= \log p(\textbf{x})+\mathbb{E}_q\Big[ \log \frac{q(\textbf{z})}{p(\textbf{z},\textbf{x})}\Big]\\ &= \log p(\textbf{x})-\mathbb{E}_q\Big[ \log \frac{p(\textbf{z},\textbf{x})}{q(\textbf{z})}\Big] \end{split} \end{align} $$
We can see that the evidence \(p(\textbf{x})\) shows up after expanding the definition of the divergence. In order to be able to perform the optimization we define the Evidence Lower Bound.
The Evidence Lower Bound (ELBO)
Let’s pause and focus on the last equivalence in eq. \((5)\). We can see that the \(\text{KL}\) divergence is equal to the marginal log-likelihood \(\log p(\textbf{x})\) plus a second term. Given that we are optimizing on \(q(\textbf{z})\), the marginal log-likelihood is a constant for the optimization. From there, it’s not difficult to conclude that minimizing \(\text{KL}\) is the same as maximizing the second term. We define the second term as the Evidence Lower Bound or ELBO.
$$ \begin{equation} \text{ELBO}(q)=\mathbb{E}_q[\log p(\textbf{x}, \textbf{z})] - \mathbb{E}_q[\log q(\textbf{z})] \end{equation} $$
ELBO has some interesting properties. First, we can rewrite ELBO expanding the joint probability as the sum of the expected log-likelihood and the \(\text{KL}\) between the variational prior \(q(\textbf{z})\) and the true prior \(p(\textbf{z})\).
$$ \begin{align} \begin{split} \text{ELBO} &= \mathbb{E}_q[\log p(\textbf{z})] + \mathbb{E}_q[\log p(\textbf{x|z})] - \mathbb{E}_q[\log q(\textbf{z})]\\ &=\mathbb{E}_q[\log p(\textbf{x|z})] - \text{KL}(\log p(\textbf{z})||q(\textbf{z})) \end{split} \end{align} $$
This allows us to better interpret what implies maximizing ELBO. On the one hand, the expected log-likelihood \(\mathbb{E}_q[\log p(\textbf{x|z})]\) pushes the distribution \(q(\textbf{z})\) towards values of \(\textbf{z}\) that explain the observable data. On the other hand, the second term \(\text{KL}(\log p(\textbf{z})||q(\textbf{z}))\) looks for a variational density \(q(\textbf{z})\) similar to the prior \(p(\textbf{z})\).
Another interesting property is that, as its name indicates, it sets a lower bound on the marginal log-likelihood. This comes from the fact that \(\text{KL}(\cdot)\) is always positive. Using this fact, ELBO is used as a model selection under the premise that the bound is a good approximation of the marginal likelihood, providing a basis for selecting a model.
$$ \begin{align} \begin{split} \text{KL} =\log p(\textbf{x}) - \text{ELBO} \geq 0\\ \Rightarrow \log p(\textbf{x}) \geq \text{ELBO} \end{split} \end{align} $$
Conclusion
The main takeaway is that the Variational Inference framework transforms the Bayesian Inference estimation into an optimization problem, maximizing the evidence lower bound. Compare to the sampling frameworks as MCMC, It provides fast and deterministic alternatives for the estimation of complex probability densities. Variational Inference is a base algorithm for Bayesian learning models as are Variational Autoencoder, Bayesian Neural Networks and Normalizing Flows.
References
[1] Blei, David M., Alp Kucukelbir, and Jon D. McAuliffe. “Variational inference: A review for statisticians.” Journal of the American statistical Association 112.518 (2017): 859-877.
[2] Jordan, Michael I., et al. “An introduction to variational methods for graphical models.” Machine learning 37.2 (1999): 183-233.
[3] Gunapati, Geetakrishnasai, et al. “Variational inference as an alternative to mcmc for parameter estimation and model selection.” Publications of the Astronomical Society of Australia 39 (2022).
[4] Ormerod, John T., and Matt P. Wand. “Explaining variational approximations.” The American Statistician 64.2 (2010): 140-153.
[5] Doersch, Carl. “Tutorial on variational autoencoders.” arXiv preprint arXiv:1606.05908 (2016).
[6] Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013).